So you have a need, a need for a particular routine. Well it just may be here.
Square Calculator
This routine calculates the 16-bit unsigned integer square of a signed 16-bit integer in the range +/-255 (decimal).
; by Lee Davison; Calculates the 16 bit unsigned integer square of the signed
; 16 bit integer in Numberl/Numberh.
; The result is always in the range 0 to 65025 and is held in Squarel/Squareh
;
; The maximum input range is only +/-255 and no checking is done to ensure that
; this is so.
;
; This routine is useful if you are trying to draw circles as for any circle
;
; x^2+y^2=r^2 where x and y are the co-ordinates of any point on the circle and
; r is the circle radius
;
; Destroys all registers
.ORG 8000 ; these must be in RAM
Numberl ; number to square low byte
Numberh = Numberl+ ; number to square high byte
.word $FFFF
Squarel ; square low byte
Squareh = Squarel+1 ; square high byte
.word $FFFF
Tempsq ; temp byte for intermediate result
.byte $00
.ORG 8192 ; any address will do
Square
LDA #$00 ; clear A
STA Squarel ; clear square low byte
; (the high byte gets shifted out)
LDA Numberl ; get number low byte
LDX Numberh ; get number high byte
BPL NoNneg ; if +ve don't negate it
; else do a two's complement
EOR #$FF ; invert
SEC ; +1
ADC #$00 ; and add it
NoNneg:
STA Tempsq ; save ABS(number)
LDX #$08 ; set bit count
Nextr2bit:
ASL Squarel ; low byte *2
ROL Squareh ; high byte *2+carry from low
ASL A ; shift number byte
BCC NoSqadd ; don't do add if C = 0
TAY ; save A
CLC ; clear carry for add
LDA Tempsq ; get number
ADC Squarel ; add number^2 low byte
STA Squarel ; save number^2 low byte
LDA #$00 ; clear A
ADC Squareh ; add number^2 high byte
STA Squareh ; save number^2 high byte
TYA ; get A back
NoSqadd:
DEX ; decrement bit count
BNE Nextr2bit ; go do next bit
RTS
Square Root Calculator
This routine calculates the 8-bit integer square root and 9 bit integer remainder of an unsigned 16-bit integer.
; by Lee Davison
; Calculates the 8 bit root and 9 bit remainder of a 16 bit unsigned integer in
; Numberl/Numberh. The result is always in the range 0 to 255 and is held in
; Root, the remainder is in the range 0 to 511 and is held in Reml/Remh
;
; partial results are held in templ/temph
;
; This routine is the complement to the integer square program.
;
; Destroys A, X registers.
; variables - must be in RAM
Numberl = $F0 ; number to find square root of low byte
Numberh = Numberl+1 ; number to find square root of high byte
Reml = $F2 ; remainder low byte
Remh = Reml+1 ; remainder high byte
templ = $F4 ; temp partial low byte
temph = templ+1 ; temp partial high byte
Root = $F6 ; square root
*= $8000 ; can be anywhere, ROM or RAM
SqRoot
LDA #$00 ; clear A
STA Reml ; clear remainder low byte
STA Remh ; clear remainder high byte
STA Root ; clear Root
LDX #$08 ; 8 pairs of bits to do
Loop
ASL Root ; Root = Root * 2
ASL Numberl ; shift highest bit of number ..
ROL Numberh ;
ROL Reml ; .. into remainder
ROL Remh ;
ASL Numberl ; shift highest bit of number ..
ROL Numberh ;
ROL Reml ; .. into remainder
ROL Remh ;
LDA Root ; copy Root ..
STA templ ; .. to templ
LDA #$00 ; clear byte
STA temph ; clear temp high byte
SEC ; +1
ROL templ ; temp = temp * 2 + 1
ROL temph ;
LDA Remh ; get remainder high byte
CMP temph ; comapre with partial high byte
BCC Next ; skip sub if remainder high byte smaller
BNE Subtr ; do sub if <> (must be remainder>partial !)
LDA Reml ; get remainder low byte
CMP templ ; comapre with partial low byte
BCC Next ; skip sub if remainder low byte smaller
; else remainder>=partial so subtract then
; and add 1 to root. carry is always set here
Subtr
LDA Reml ; get remainder low byte
SBC templ ; subtract partial low byte
STA Reml ; save remainder low byte
LDA Remh ; get remainder high byte
SBC temph ; subtract partial high byte
STA Remh ; save remainder high byte
INC Root ; increment Root
Next
DEX ; decrement bit pair count
BNE Loop ; loop if not all done
RTS
256-Byte Data Buffer
This routine is an interrupt serviced 256 byte data buffer for serial ports and the like.
Very similar code was used to supply the stepper motor driver routine with line co-ordinate pairs.
This is not a finished solution, you will need to add your own code to drive the target of the buffer.
; By Lee Davison
; code for an interrupt serviced data buffer. similar code is used to drive
; the XY stepper motors on a plotter with new position information every 5mS
; and also to allow pen up/down movement time of 70mS
; buffer and variables must be in RAM
Buffer ; 256 byte buffer (must start at page edge)
.ds $100
BRindx ; buffer read index
.byte $00
BWindx ; buffer write index
.byte $00
Sendf ; am sending flag
.byte $00
WByte ; temp store for the byte to be sent
.byte $00
; write the data to the buffer a byte at a time and increment the pointer.
; the routine is called with the byte to write in A. If the interrupt
; device is idle when this routine is called it will wake it up by doing
; a BRK before it exits
; destroys the Y register
; can be ROM or RAM
Incwritb
STA WByte ; save byte to write
LDA BRindx ; get read index
SEC ; set carry for subtract
SBC BWindx ; subtract write index
BEQ Dowrite ; if equal then buffer empty so do write
CMP #$02 ; need at least n+1 bytes to avoid rollover
BCC Incwritb ; loop if no space
; construct and write data to buffer
Dowrite
LDY BWindx ; get write index
LDA WByte ; get byte to write
STA Buffer,Y ; save it
INY ; increment index to next byte
STY BWindx ; save new write index byte
; now see if the interrupt service routine is already running or if it's
; idle
LDA Sendf ; get the sending flag
BNE Doingit ; skip call if running
BRK ; software call to interrupt routine
NOP ; need this as return from BRK is +1 byte!
CLI ; enable the interrupts
Doingit
RTS
; this is the interrupt service routine. takes a byte a time from the
; buffer and does some thing with it. also sets up the device(s) for
; the next interrupt
; no registers altered
BuffIRQ
PHA ; save A
TXA ; copy X
PHA ; save X
TYA ; copy Y
PHA ; save Y
; insert code here to ensure this is the interrupt you want. if it
; isn't then just exit quietly via ResExit the end of the routine
Getnext
JSR Increadb ; increment pointer and read byte from buffer
BCS ExitIRQ ; branch if no byte to do
; here would be the guts of the routine such as sending the byte to
; the ACIA or a printer port or some other byte device. it will also
; ensure the device is set to generate an interrupt when it's completed
; it's task
LDA #$FF ; set byte
STA Sendf ; set sending flag
JMP ResExit ; restore the registers & exit
; all done, clear the flag restore the
; registers & exit
ExitIRQ
LDA #$00 ; clear byte
STA Sendf ; clear sending flag
ResExit
PLA ; pull Y
TAY ; restore it
PLA ; pull X
TAX ; restore it
PLA ; restore A
RTI ; this was an interrupt service request
; so exit properly
; get byte from the buffer and increment the pointer. If the buffer is empty
; then exit with the carry flag set else exit with carry clear and the byte
; in A
Increadb
LDY BRindx ; get buffer read index
CPY BWindx ; compare write index
BEQ NOktoread ; branch if empty (= sets carry)
LDA Buffer,Y ; get byte from buffer
INY ; increment pointer
STY BRindx ; save buffer read index
CLC ; clear not ok flag
NOktoread
RTS
6502 8 bit PRNG
This is a short piece of code that generates a maximal length, 8 bit, pseudo random
number sequence. This routine is no great shakes in the speed stakes, it’s just a demo of a usefull
technique.
; by Lee Davison
; returns pseudo random 8 bit number in A. Affects A, X and Y.
; (r_seed) is the byte from which the number is generated and MUST be
; initialised to a non zero value or this function will always return
; zero. Also r_seed must be in RAM, you can see why......
rand_8
LDA r_seed ; get seed
AND #$B8 ; mask non feedback bits
; for maximal length run with 8 bits we need
; taps at b7, b5, b4 and b3
LDX #$05 ; bit count (shift top 5 bits)
LDY #$00 ; clear feedback count
F_loop
ASL A ; shift bit into carry
BCC bit_clr ; branch if bit = 0
INY ; increment feedback count (b0 is XOR all the
; shifted bits from A)
bit_clr
DEX ; decrement count
BNE F_loop ; loop if not all done
no_clr
TYA ; copy feedback count
LSR A ; bit 0 into Cb
LDA r_seed ; get seed back
ROL A ; rotate carry into byte
STA r_seed ; save number as next seed
RTS ; done
r_seed
.byte 1 ; prng seed byte (must not be zero)
Other number lengths
A maximal length pseudo random number generator is basically just a shif register with feedback from the later stages to generate the next input bit. The form for a generator of length n with feedback from t is shown below.
Pseudo random sequence generator
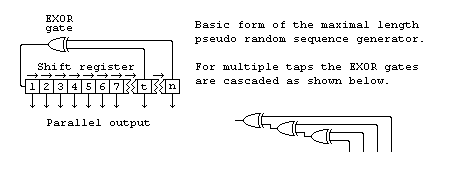
You don’t have to limit the length to only 8 bits, any number of bits from two upwards will work if you chose the right feedback tap(s). Here is a table of some values.
| Bits [n] |
Tap(s) [t] |
Length |
Bits [n] |
Tap(s) [t] |
Length |
| 2 |
1 |
3 |
3 |
2 |
7 |
| 4 |
3 |
15 |
5 |
3 |
31 |
| 6 |
5 |
63 |
7 |
6 |
127 |
| 8 |
6,5,4 |
255 |
9 |
5 |
511 |
| 10 |
7 |
1023 |
11 |
9 |
2047 |
| 15 |
14 |
32767 |
16 |
15,13,4 |
65535 |
| 17 |
14 |
131071 |
18 |
11 |
262143 |
| 20 |
17 |
1048575 |
21 |
19 |
2097151 |
| 22 |
21 |
4194303 |
23 |
18 |
8388607 |
| 24 |
23,22,17 |
16777215 |
25 |
22 |
33554431 |
| 28 |
25 |
268435455 |
29 |
27 |
536870911 |
| 31 |
28 |
2147483647 |
|
|
|
In the last case, with 31 bits, if you took a new value once a second the sequence
wouldn’t repeat for over sixty eight years. Even clocked at 1MHz it would still take
over thirty five minutes to cycle through every state.
Faster, shorter method
The above pseudo random number generator is known as a Fibonacci generator and, while it works, it turns out there is a much better generator to implement with a microprocessor.
Galois pseudo random sequence generator.
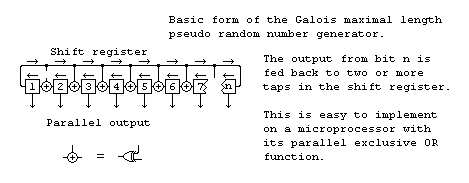
The Galois generator needs only to test the state of one bit and that can be tested after
the shift has been performed. The state of this bit determines whether the feedback term
is exclusive ORed with the result. This single bit test and multiple bit feedback is
easily done as can be seen from the code below.
; returns pseudo random 8 bit number in A. Affects A. (r_seed) is the
; byte from which the number is generated and MUST be initialised to a
; non zero value or this function will always return zero. Also r_seed
; must be in RAM, you can see why......
rand_8
LDA r_seed ; get seed
ASL ; shift byte
BCC no_eor ; branch if no carry
EOR #$CF ; else EOR with $CF
no_eor
STA r_seed ; save number as next seed
RTS ; done
r_seed
.byte 1 ; prng seed byte, must not be zero
You don’t have to limit the length to only 8 bits, any number of bits from three upwards will work if you chose the right feedback value. Here is a table of some values that have been chosen to give a feedback value that fits in a byte, this makes implementation on an 8 bit micro as short as possible. For these values bit n is the least significant bit in the value and the tested bit is the bit shifted out from bit 1.
| Bits [n] |
Feedback |
Length |
Bits [n] |
Feedback |
Length |
| 3 |
$03 |
7 |
4 |
$03 |
15 |
| 5 |
$17 |
31 |
6 |
$27 |
63 |
| 7 |
$4B |
127 |
8 |
$CF |
255 |
| 9 |
$B7 |
511 |
10 |
$E7 |
1023 |
| 11 |
$EB |
2047 |
12 |
$EB |
4095 |
| 13 |
$BB |
8191 |
14 |
$BB |
16383 |
| 15 |
$DD |
32767 |
16 |
$D7 |
65535 |
| 17 |
$AF |
131071 |
18 |
$E7 |
262143 |
| 19 |
$AF |
524287 |
20 |
$F3 |
1048575 |
| 21 |
$B7 |
2097151 |
22 |
$BB |
4194303 |
| 23 |
$F3 |
8388607 |
24 |
$DB |
16777215 |
| 25 |
$93 |
33554431 |
26 |
$B1 |
67108863 |
| 27 |
$B1 |
134217727 |
28 |
$E1 |
268435455 |
| 29 |
$C3 |
536870911 |
30 |
$AF |
1073741823 |
| 31 |
$8B |
2147483647 |
32 |
$AF |
4294967295 |
This is now the form of sequence generator used to generate values for the RND() function in EhBASIC.
“The generation of random numbers is too important to be left to chance.”
Robert R. Coveyou.
 Enhanced BASIC is a BASIC interpreter for the 6502 and compatible microprocessors. It is constructed to be quick and powerful and easily ported to most 6502 systems. It requires few resources to run and includes instructions to facilitate easy low level handling of hardware devices. It also retains most of the powerful high level instructions from similar BASICs.
Enhanced BASIC is a BASIC interpreter for the 6502 and compatible microprocessors. It is constructed to be quick and powerful and easily ported to most 6502 systems. It requires few resources to run and includes instructions to facilitate easy low level handling of hardware devices. It also retains most of the powerful high level instructions from similar BASICs.