 6502 Shorts by Lee Davison
6502 Shorts by Lee Davison
This section is for those short bits of code that are just what you need every now and then.
Toggle carry – Change the sense of the carry bit.
Carry bit the wrong sense? Want a 0 when it’s 1? Read on….
The code
Recently in some otherwise elegant code the result of a compare left the carry bit in
exactly the wrong sense for the following add. The usual way to fix that is to do
something like ..
BCC WasClear ; if clear go set it CLC ; was set so clear it BCC AllDone ; continue WasClear SEC ; was clear so set it AllDone
While this works there had to be a more elegant way of doing this. It turns out there is, you do this ..
ROL A ; Cb into b0 EOR #$01 ; toggle bit ROR A ; b0 into Cb
The ROL puts the carry into bit 0 in the accumulator.
The EOR toggles the state of that bit without affecting any other bits.
The ROR puts the bit back into the carry, restores the accumulator and sets the N and Z flags.
There are a couple of advantages of doing things this way instead of the branch and set (or clear) given earlier ..
It only takes four bytes instead of six. It always takes six cycles, not five or seven depending on the state of the carry.
There is one possible disadvantage in that it sets the N and Z flags from what is in A at the time. But, most of the time, if you’re interested in the carry state the N and Z states are unimportant.
Range test – Test a byte is in the range n to m
Sometimes you need to check if a byte is in a certain range that does not start,
or end, on the byte limits. For example, if a byte is numeric (n = ‘0’, m = ‘9’)
or lower case ASCII (n = ‘a’, m = ‘z’).
For all of these we assume that the byte to be tested is in A and that the start and end values, n and m, are already defined. Also that 0 < n < m < $FF.
If you don’t need to preserve the byte in A then testing the byte can be done in five bytes and only six cycles. This sets the carry if A is in the range n to m.
CLC ; clear carry for add ADC #$FF-m ; make m = $FF ADC #m-n+1 ; carry set if in range n to m
If you want the carry clear instead of set you use subtract instead of add.
SEC ; set carry for subtract SBC #n ; make n = $00 SBC #m-n+1 ; carry clear if in range n to m
If you need to preserve A and have either the X or Y register free you can do it like this.
TAX ; copy A (or TAY) CLC ; clear carry for add ADC #$FF-m ; make m = $FF ADC #m-n+1 ; carry set if in range n to m TXA ; restore A (or TYA)
If you can spare the cycles but not the registers then this is the slowest of the range tests coming in at thirteen cycles.
PHA ; save A CLC ; clear carry for add ADC #$FF-m ; make m = $FF ADC #m-n+1 ; carry set if in range n to m PLA ; restore A
Finally a method that preserves A without using any other registers, or memory.
This has the disadvantage that it can take either five or ten cycles (so timing
would be unsure) and takes the most bytes. This one sets the carry if A is in the
range n to m.
CMP #n ; is it less than required? BCC ERnge ; branch if it is ADC #$FE-m ; add $FF-m (carry is set) CLC ; clear carry for add ADC #m+1 ; A is now back to original value ERnge
And this one clears the carry if A is in the range n to m.
CMP #m+1 ; is it greater than required? BCS ERnge ; branch if it is SBC #n-1 ; subtract n (carry is clear) SEC ; set carry for subtract SBC #-n ; A is now back to original value ERnge
BCD to binary – Convert a BCD byte to binary
I don’t think this will win any prizes but it works (which is always a bonus). The byte temp can be anywhere but is probably best in page zero.
TAX ; copy BCD value AND #$F0 ; mask top nibble LSR ; /2 (/16*8) STA temp ; save it LSR ; /4 (/16*4) LSR ; /8 (/16*2) ADC temp ; add /2 (carry always clear) ; ((n/16*8)+(n/16*2) = (n/16*10)) STA temp ; save it TXA ; get original back AND #$0F ; mask low nibble ADC temp ; add shifted (carry always clear)
This is seventeen bytes long (assuming temp is in page 0) which makes it just about the
right size for this section.
There is no error checking and it is up to the calling routine to ensure that the source byte is a valid BCD byte. If it isn’t nothing bad happens, you just get the sum of the low nibble and the high nibble times ten.
Binary to BCD – Convert a binary byte to BCD
Another one I’d not thought about until recently when I was asked if I had it. Here’s what I eventually came up with….
I know it’s almost a bit long for this section but it is the complement to the BCD to binary r
The byte to be converted is in A and the result is returned in low(/high) and A(/X).
The bytes low and high can be anywhere but are probably best in page zero.
If you know that the value to be converted lies in the range $00 to $63 (0 to 99 decimal)then all the code between the ***** lines can be omitted.
; table of BCD values for each binary bit, put this somewhere. ; note! values are -1 as the ADC is always done with the carry set b2b_table .byte $63,$31,$15,$07,$03,$01,$00 bin_2_bcd SED ; all adds in decimal mode STA low ; save A LDA #$00 ; clear A LDX #$07 ; set bit count bit_loop LSR low ; bit to carry BCC skip_add ; branch if no add ADC b2b_table-1,X ; else add BCD value skip_add DEX ; decrement bit count BNE bit_loop ; loop if more to do ;*********************************************************************** ; if you only require conversion of numbers between $00 and $63 (0 to 99 ; decimal) then omit all code between the "*"s BCC skip_100 ; branch if no 100's carry ; if Cb set here (and can only be set by the ; last loop add) then there was a carry into INX ; the 100's so add 100's carry to the high byte skip_100 ; now check the 2^7 (128) bit LSR low ; bit 7 to carry BCC skip_fin ; branch if no add INX ; else effectively add 100 part of 128 ADC #$27 ; and then add 128 (-1) part of 128 BCC skip_fin ; branch if no further carry INX ; else add 200's carry skip_fin STX high ; save result high byte ; end of 100's code ;*********************************************************************** STA low ; save result low byte CLD ; clear decimal mode
The two BCD digit version is $1C bytes long (assuming temp is in page zero) including the table which means it just about makes it small enough for this section.
There is no error checking and it is up to the calling routine to ensure that the source byte will become a valid BCD byte or word.
Hex to ASCII – Another way to convert a hex nibble
I know you’ve all done this before but here’s a use for decimal mode. Read on….
The classic way to convert a nibble in A into ASCII is to test if the nibble is greater than nine and, if it is, to add seven before adding the 48 to make the ASCII character.
CMP #$0A ; set carry for +1 if >9 BCC NoAdjust ; branch if <=9 ADC #6 ; adjust if A to F ; (six plus carry = 7!) NoAdjust ADC #"0" ; add ASCII "0"
This is eight bytes long and takes seven or eight cycles depending on the nibble.
Well here’s a way that uses decimal mode addition to do that for you.
SED ; set decimal mode CMP #$0A ; set carry for +1 if >9 ADC #"0" ; add ASCII "0" CLD ; clear decimal mode
Six bytes and always nine cycles. Or, if you do a number of nibbles and leave decimal mode set throughout, four bytes and five cycles per digit.
Another way
Following some posts on the classiccmp mailing list this became obvious. It’s not fast or short (really too long for this section but I’ll let it pass) but it doesn’t use branches, decimal mode or other registers or memory.
CMP #$0A ; compare the nibble with $0A ADC #$00 ; add 1 if it was >= $0A CMP #$0A ; compare the nibble with $0A ADC #$00 ; add 1 if it was >= $0A CMP #$0A ; compare the nibble with $0A ADC #$00 ; add 1 if it was >= $0A CMP #$0A ; compare the nibble with $0A ADC #$00 ; add 1 if it was >= $0A CMP #$0A ; compare the nibble with $0A ADC #$00 ; add 1 if it was >= $0A CMP #$0A ; compare the nibble with $0A ADC #$00 ; add 1 if it was >= $0A CMP #$0A ; compare the nibble with $0A ADC #"0" ; add "0" and 1 if it was >= $0A
Twenty eight bytes and twenty eight cycles, only really usefull for a ‘convert hex to ASCII without using branches, decimal mode or look up tables’ competition.
Yet another way. Last one, honest. Not the shortest but this must be the fastest way. Starts with the nibble to be converted in X not A
LDA hex_table,X ; get the ASCII character . hex_table .byte "0123456789ABCDEF" ; conversion table
Nineteen bytes, eighteen if the table is in page zero, and only four cycles. Speedy!
Check CMOS – Test if code is running on a 65C02
Nothing particularly fancy, the code simply makes use of the fact that the NMOS 6502 does not set the zero flag bit when doing decimal adds or subtracts and the CMOS 6502 does. The result of this is that Zb is set only if the code is run on a CMOS 6502.
SED ; set decimal mode CLC ; clear carry for add LDA #$99 ; actually 99 decimal in this case ADC #$01 ; +1 gives 00 and sets Zb on 65C02 CLD ; exit decimal mode
Enjoy.
Save XY – Push/pull X & Y without using A
Not something that comes up very often. I needed some code that would run on an NMOS 6502, not destroy X or Y, return a value in A and was re-entrant, i.e. it could call itself without overwriting any values.
First we save all the registers. We’re not really interested in the value of A but we need a byte on the stack.
PHA ; make space for A TYA ; copy Y PHA ; save Y TXA ; copy X PHA ; save X
Now we have to restore the registers. Because we don’t have PHX/PLX or PHY/PLY we must use A to restore X and Y but we also don’t want to overwrite A, we can’t just push A onto the stack as that makes getting X and Y off something of a problem. What we do is to overwrite the value for A that is already on the stack and then just pop the registers as we normally would.
TSX ; copy stack pointer STA $0103,X ; write result to stacked A PLA ; pull stacked X TAX ; restore X PLA ; pull stacked Y TAY ; restore Y PLA ; get result into A
This code is also usefull if you don’t know which type of 6502 the code will be run on and you need it to work on all of them.
Update .. need it to work on all of them. Or not as it turns out. There can be a case when the above code doesn’t work and that is if the stack is nearly full when the code is entered. While this won’t happen very often, it happen and code that works all the time can be frustrating.
Let’s look at what happens when it fails, first the code as it saves the registers ..
<b> S Address</b> PHA $02 <span style="color: blue;"><b>$0102</b></span> ; make space for A TYA $01 ..... ; copy Y PHA $01 $0101 ; save Y TXA $00 ..... ; copy X PHA $00 $0100 ; save X <i><more code></i> $FF $01FF ; subroutine code
In this case A was pushed to address $0102 but after pushing X and Y the stack is full and the stack pointer now points back to the top of the stack. Now when the code tries to save A and exit the following happens ..
<b> X Address</b> TSX $FF ..... ; copy stack pointer STA $0103,X $FF <span style="color: red;"><b>$0202</b></span> ; write result to stacked A <b> S Address</b> PLA $00 $0100 ; pull stacked X TAX $01 ..... ; restore X PLA $01 $0101 ; pull stacked Y TAY $02 ..... ; restore Y PLA $02 <span style="color: blue;"><b>$0102</b></span> ; get result into A
Oops! We just failed to return the value in A and trashed $0202 as well. The solution is to make X equal the stack pointer when A was first pushed and use this as the offset from the base of the stack page.
TSX ; copy stack pointer INX ; increment X to .. INX ; .. equal stack pointer .. INX ; .. when A was pushed STA $0100,X ; write result to stacked A PLA ; pull stacked X TAX ; restore X PLA ; pull stacked Y TAY ; restore Y PLA ; get result into A
Now going through the code showing the register values ..
<b> X Address</b> TSX $FF ..... ; copy stack pointer INX $00 ..... ; increment X to .. INX $01 ..... ; .. equal stack pointer .. INX $02 ..... ; .. when A was pushed STA $0100,X $02 <span style="color: green;"><b>$0102</b></span> ; write result to stacked A <b> S Address</b> PLA $00 $0100 ; pull stacked X TAX $01 ..... ; restore X PLA $01 $0101 ; pull stacked Y TAY $02 ..... ; restore Y PLA $02 <span style="color: blue;"><b>$0102</b></span> ; get result into A
This costs a few bytes and some clock cycles but will work even if the stack pointer should wrap as above.
Eight bit rotates – One bit less in ROL or ROR
ROR and ROL both rotate a byte through the carry giving, in effect, a nine bit rotate. Sometimes an eight bit rotate is needed, as shown in the diagram below.
Here is a way to make those rotates effectively eight bit.
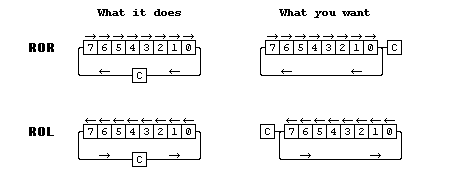
To make ROR an eight bit shift b0 must be duplicated in the carry bit, the easiest way to do this is to shift the byte but that alters it so first make a copy, rotate the byte, restore the copy and do the eight bit rotate thus ..
TAX ; save byte ROR A ; b0 into Cb TXA ; restore byte ROR A ; eight bit rotate
Not particularly elegant but does have the advantage that it takes the same number of cycles whatever the state of b0 before the rotate. If no register is available the stack can be used instead like this ..
PHA ; save byte ROR A ; b0 into Cb PLA ; restore byte ROR A ; eight bit rotate
To make ROL behave like an 8 bit shift the sense of the sign bit must be reflected in the carry bit before the shift is done. this is much easier and can be done thus ..
CMP #$80 ; copy b7 into Cb ROL A ; eight bit rotate
ASL & ASR – A true arithmetic shift left and right
Though the 6502 instruction set has an instruction that is called Arithmetic Shift Left it is really only a Logical Shift Left as the overflow bit is not affected if there is a sign change. To perform a true arithmetic shift the state of the sign before and after the shift must be taken into account. There is no Arithmetic shift right.
The code – Arithmetic Shift Left.
To perform a true Arithmetic Shift Left an add can be used instead ..
CLC ; clear the carry for a single byte shift STA temp ; copy A ADC temp ; effectively perform a true ASL
.. which looks like a long way to go about it but the overflow bit is set if the sign bit has been changed by the shift.
A multiple byte Arithmetic Shift Left can be done like this ..
ASL lsb ; shift the least significant byte ROL inter ; shift any intermediate byte(s) ... LDA msb ; copy the most significant byte ADC msb ; effectively perform a true ASL STA msb ; save the most significant byte
In this case the overflow bit is only needed for the most significant byte so the less significant bytes can be shifted using shift instructions.
The code – Arithmetic Shift Right.
To perform an Arithmetic Shift Right the state of the sign bit needs to be copied to the carry bit before the shift ..
CMP #$80 ; copy the sign bit to the carry bit
ROR A ; effectively perform a true ASR
Unlike the left shift there is no possibility of an overflow during a right shift.
Sign extend – Extending a less than 8 bit value to 8 bits
Sometimes you end up with a signed value that is not in a multiple of 8 bits, the problem then is to extend the sign to fill the most significant byte.
For example, a signed value is in bits 4 to 0 of the Accumulator and is to be extended to to fill all eight ..
AND #$1F ; clear any unused bits CLC ; clear the carry for an add ADC #$F0 ; set top bits clear if -ve, set if +ve EOR #$F0 ; toggle bits to the correct state
Using a suitable mask, if needed, and add value this works to extend the sign for any bit in the byte.
